こんにちは。就活無双です。
今回は玉手箱の空欄推測(推論)の解き方のコツを伝授していきます。
空欄推測(推定)の解き方のコツ【完全版】
玉手箱の 空欄推測(推論) とは?
玉手箱の『非言語』の問題の1種類です。『非言語』には、『計数』『空欄推測(推論)』『四則演算』の3種類があります。『?』に当てはまる値を、柔軟な思考力で求める、パズルのような問題を玉手箱の 『空欄推測(推論)』 と言います。
20問20分と35問35分の2種類があります。
玉手箱の 空欄推測(推論) の難易度は?
他のWEBテストと比較すると、非常に難しいです。時間内に全て問題を解くのは困難でしょう。
しかし、全ての問題数が多くはありません。
そのため、回数をこなすことで同じ問題が出る可能性が高くなりやすい部類のWEBテストです。
玉手箱の 空欄推測(推論) の高得点の目安は?
企業や業界にもよりますが、8割の正答率があれば問題ありません。
『8割も必要なの?』と疑問に持たれる方もいるかも知れませんが、 空欄推測(推論) を採用している企業を受ける学生はそもそものレベルが高いので、8割は必要といえます。
玉手箱の 空欄推測(推論)を採用している企業
多くはないですが、特に優秀な学生を求める企業は採用しています。
特にコンサル業界では多く採用されています。
2022年度は、みずほFGやアクセンチュア、NTT東日本、SMBCグループ、野村證券、日本総研などの企業で採用されていました。
2024年度 玉手箱 空欄推測 採用企業 ・アクセンチュア ・みずほFG ・SMCC ・SMFL ・SMBC ・SMBC日興証券 ・日本総研 ・川崎汽船 ・千代田化工建設 ・オリックス ・NTT東日本 ※2025年度採用では変更される可能性もあるので、参考までに。
空欄推測(推論)の種類は6つ

①比例
『ある項目が別の項目の何倍』という比例の関係になっている問題
例1 あるサッカー場で行われた3日間の試合のチケット売上枚数を集計しています。
| 1日目 | 2日目 | 3日目 | |
| チケット売上枚数(枚) | 400 | 680 | 900 |
| 飲料売上額(円) | 1200 | 2040 | ? |
3日目のチケット売上枚数は何枚と推測できるか。
○2400枚 ○2700枚 ○3300枚 ○3400枚 ○3700枚
答え 2700枚 (法則)1日目も2日目も、飲料売上額がチケット売上枚数の3倍になっている。 従って、900×3=2700(枚)
②挟み込み
『?』が別の2つの値に挟まれている。計算を行わずに、答えを求めることができる。
例2 あるチェーン店居酒屋で、3月の各店舗の売上実績をまとめました。
| A店 | B店 | C店 | D店 | E店 | |
| 売上目標(万円) | 600 | 670 | 890 | 820 | 730 |
| 売上実績(万円) | 583 | 634 | 855 | 749 | ? |
| 従業員数(人) | 18 | 18 | 30 | 24 | 27 |
E店の売上実績はいくらと推測できるか。
○540万円 ○631万円 ○674万円 ○781万円 ○823万円
答え 674万円 (法則)売上目標が大きい店舗ほど、売上実績も大きい。 E店の売上目標(730)はB店(670)とD店(820)の間である。 従って、E店の売上実績はB店(634)~D店(749)の間であるので674万円
③計算
いくつかの項目を使い、法則性を導き出し『?』を計算するもの。
例3 あるガラス食器メーカーでは、4つの工房でオリジナル製品を作っています。
| A工房 | B工房 | C工房 | D工房 | |
| 材料費(万円) | 420 | 450 | 500 | 480 |
| スタッフ数(人) | 5 | 8 | 10 | 9 |
| 利益(万円) | 2580 | 4350 | 5500 | ? |
D工場の利益はいくらと推測できるか。
○2800万円 ○3650万円 ○4200万円 ○4920万円 ○5300万円
答え 4920万円 (法則)スタッフ数×600-材料費=利益となっている。 従って、9×600-480=4920万円
④変化
『 何日経過ごとに、いくら増える 』といった、数の変化に法則性があるもの
例4 あるレンタルビデオショップのビデオの延滞日数と延滞料金の規定です。
| 延滞日数(日) | 1 | 4 | 7 | 10 | 13 |
| 延滞料金(円) | 300 | 900 | 1500 | 2100 | ? |
13日延滞した際の延滞料金はいくらと推測できるか。
○2200円 ○2300円 ○2400円 ○2600円 ○2700円
答え 2700円 (法則)延滞日数が3日増えると、延滞料金が600円増加している。 従って、2100+600=2700円
⑤合計が等しい
いくつかの項目の合計が、常に一定であるというもの
例5 ある家電量販店で、エアコンの購入者に対して、エアコンを知った媒体についてアンケートを取っています。
| エアコンA | エアコンB | エアコンC | エアコンD | エアコンE | |
| 新聞折込チラシ(人) | 20 | 30 | 20 | 32 | 12 |
| テレビCM(人) | 32 | 21 | 21 | 23 | 10 |
| ダイレクトメール(人) | 2 | 3 | 2 | 2 | 6 |
| WEBサイト(人) | 42 | 35 | 50 | 12 | 30 |
| 店頭(人) | 28 | 35 | 20 | 58 | ? |
エアコンEを店頭で知って購入した人は何人と推測することができるか?
○28人 ○30人 ○36人 ○40人 ○45人
答え 40人 (法則)WEBサイトと店頭の合計が常に70である。 従って、70-30=40人
⑥列で考えるパターン
変数は多いが、いくつかの項目を足して、項目数で割ると簡単に答えを求められるもの
例6 以下は、駄菓子屋のお菓子セットの料金である。
| Aセット | Bセット | Cセット | Dセット | Eセット | F セット | |
| 板チョコ(枚) | 1 | 2 | 3 | 2 | 1 | 3 |
| あめ玉(個) | 5 | 1 | 4 | 3 | 2 | 5 |
| ガム(個) | 2 | 2 | 4 | 4 | 2 | 2 |
| ポテトチップス(袋) | 1 | 3 | 1 | 2 | 1 | 2 |
| わたがし(袋) | 1 | 2 | 1 | 1 | 2 | 1 |
| 合計金額(円) | 380 | 760 | 560 | 590 | 450 | ? |
Fセットの合計金額はいくらと推測できるか。
○630円 ○640円 ○650円 ○660円 ○670人円
答え 660円 (法則)AとBとCの各お菓子の合計がDとEとFの各お菓子の合計と等しい。 (例)板チョコのA~Cの合計1+2+3=板チョコのD~Fの合計2+1+3=6 従って、A~Cの合計金額の合計はD~Fの合計金額に等しい。 380+760+560=1700.1700-(590+450)=660円
解き方のコツ
①比例
真っ先にこの『比例』を疑ってください。変数が少ない場合は、この『比例』のことが多いです。
比例は、〇倍などと目視で分かる場合が多いです。難問に時間を残しておくためにも瞬殺できるようにしておきましょう。
②挟み込み
『挟み込み』は非常に慣れが必要です。論理的に計算をして解こうとすればするほど時間がかかり、解けません。そのため、特に理系の方は注意して下さい。
『挟み込み』の場合は、答えの選択肢が刻んでいて、それぞれの値が遠い場合が多いです。
○540万円 ○631万円 ○674万円 ○781万円 ○823万円
上記の選択肢ように、1の桁が揃っておらず、100の位も揃っていません。
例2を参照
③計算
『比例』でも『挟み込み』でもない場合は、『計算』です。
しかし、法則性を見つけるのに、時間がかかる場合が多いです。
その際のコツを2つ紹介します。
コツ1 一般的な前提を参考にして法則性を導く
例えば、例3の場合だと『スタッフ一人当たりの作業量に出荷額は対応してくるだろうな』や『利益は出荷額から利益を引いた値だろうな』といった前提です。
勿論、前提がそのまま式に当てはまらない場合もありますが、大抵の場合は手掛かりになります。
コツ2 10の位や1の位に注目する
10の位 や1の位が『0』の時などは、特に注意しましょう。計算がしやすい場合が多いです。
例3の場合だと、A工房を見て、『スタッフ×600ー材料費』を導くのは困難です。
C工房の利益5500という値を見ると、『材料費の11倍?』『スタッフの数倍から材料費を引いた値?』というように比較的直ぐにいくつかの道筋を探ることができますし、計算も暗算でしやすいです。
④変化
変化は比較的分かりやすい部類です。
注意すべき点としては、増減する場合があるということです。
その場合でも、変化の絶対値は同じであることに気づけば、全く問題ありません。
⑤合計が等しい
非常に変数が多い場合は、『合計が等しい』か『列で考えるパターン』のどちらかです。
①変数が多い ②値が刻みすぎている といった特徴がある場合は、どこかの『合計が等しい』 場合が多いので、注意しましょう。
『りんごとみかんの出荷量の合計が毎年同じ』など、あまり論理的ではないものも多いので注意してください。
⑥列で考えるパターン
これは、非常に分かりやすいです。しかし、どの変数を見るべきか探すのに時間が掛かります。
『うわ、変数が多い。けど、連立方程式をいくつも立てて時間をかけて計算したら絶対に答えが出るわ』
と思ったら、ほぼ100%このパターンです。
このパターンだと分かってから、時間がかかるので、問題慣れしておくことをお勧めします。
注意すべき問題は?
圧倒的に『挟み込み』です。
非常に忘れがちですが、全体の1/5くらいはこれで解けます。
「は?これ計算で解けなくね?」って感じた時は大体挟み込みで解けます。
変数が2個とかなら割とすぐ気が付くんですが、変数が4個とかでも挟み込みのパターンあったりします。
まとめ
絶対にフィーリングで解かないで下さい。答えは1つしかありません。
空欄推測(推論)は難しいですが、その分 経験と努力で一番キャッチアップしやすいと思います 。
対策しないと、本当に大変なことになるので、時間に余裕のある時に練習しましょう。
秘密情報
始まってすぐに簡単な問題が続くパターンと、後半に簡単な問題が続くパターンがあります。
受けた回によって異なってたので、規則性はないと思いますが、序盤に難しい問題が来た場合は「後半に簡単な問題来るから時間残しておこう」と意識した方が良いです。
あと、僕が推論企業を20回くらい受けた感じでは問題の被り方からして、全部の問題数は800から1000くらいかなと感じてます。(毎年増えていくはずですが)
ちなみに、空欄推測に限らずWEBテストは【関数電卓】を利用することを強くお勧めします。
 | 価格:946円 |
練習問題を解こう!
ある花屋で、花束の見積書を作成しています。
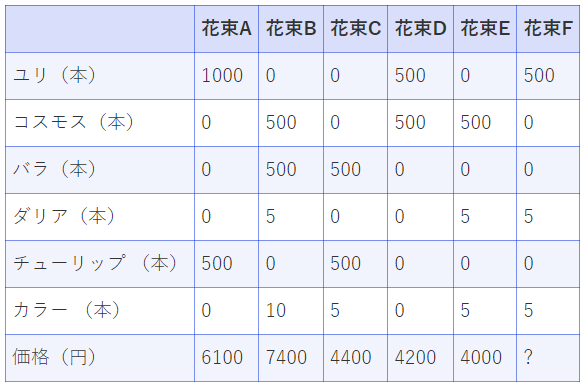
花束Fの金額はいくらと推測できるか。 ○4600円 ○4700円 ○4800円 ○4900円 ○5000円






コメント